Roulette Probability Questions

As the graph shows, the probability of seeing the same colour on consecutive spins of the roulette wheel more than halves (well, the ratio probability doubles) from one spin to the next. I stopped the graph at 6 trials/spins, as that was enough to highlight the trend and produce a prettier probability graph. Random roulette probabilities. Roulette Mathematics. If you want to excel at roulette, then you really need to understand the maths behind it. True odds are the real world chance of a certain outcome, whereas the house odds are the payout ratio for the same scenario and are typically slightly lower. As the graph shows, the probability of seeing the same colour on consecutive spins of the roulette wheel more than halves (well, the ratio probability doubles) from one spin to the next. I stopped the graph at 6 trials/spins, as that was enough to highlight the trend and produce a prettier probability graph. Random roulette probabilities.

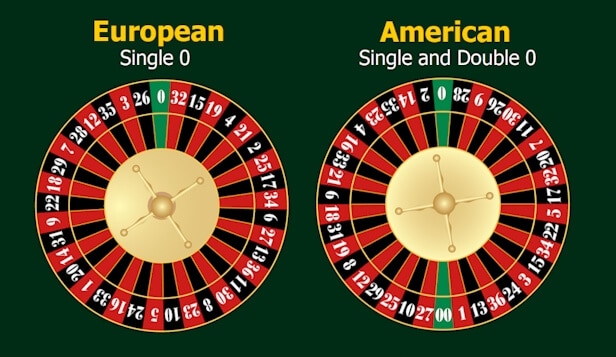
1. If we now look at the roulette game, suppose you bet $1 on the number 5 each time you play. What are the payoffs? You can either win $35 or lose $1. The probability that you win $35 is 1/38 (only one winning number out of the total of 38). The probability that you lose $1 (that is you 'win' $-1) is 37/38 (37 losing numbers out of the total of 38).
2. An American roulette wheel has 38 pockets in which the ball can land. The probability of the ball landing in a specific pocket is 1/38. This can also be expressed as 37 to 1. This is a great example, because it demonstrates how the casino gets its edge over the player. This bet pays off at 35 to 1.

.

Roulette Probability Example

.

Roulette Wheel Probability Questions

'All will be well if you use your mind for your decisions, and mind only your decisions.' Since 2007, I have devoted my life to sharing the joy of game theory and mathematics. MindYourDecisions now has over 1,000 free articles with no ads thanks to community support! Help out and get early access to posts with a pledge on Patreon.

.
.

Can probability theory save your life? Perhaps not in usual circumstances, but it sure would help if you found yourself playing a game of Russian roulette.

Today’s article covers a couple of variations on the Russian roulette puzzle, which is occasionally asked as an interview brain teaser.

Puzzle 1: Single bullet

I received this puzzle in an email:

Let’s play a game of Russian roulette. You are tied to your chair and can’t get up. Here’s a gun. Here’s the cylinder of the gun, six chambers, all empty. Now watch me as I put a single bullet in the gun. I close the cylinder and spin it. I put a gun to your head and pull the trigger. Click. Lucky you! Now I’m going to pull the trigger one more time. Which would you prefer, that I spin the cylinder first, or that I just pull the trigger?

(I’m not sure of the original source, but the wording is similar to a problem in William Poundstone’s book How Would You Move Mount Fuji?)

The problem can be solved by calculating the probability of survival for the choices.

First, consider the odds of survival if the cylinder is spun. The cylinder is equally likely to stop at any of the six chambers. One of the chambers contains the bullet and is unsafe. The other five chambers are empty and you would survive. Consequently, the probability of survival is 5/6, or about 83 percent.

Next, consider the odds if the cylinder is not spun. As the trigger was already pulled, there are five possible chambers remaining. Additionally, one of these chambers contains the bullet. That leaves four empty or safe chambers out of five. Thus the probability of survival is 4/5, or 80 percent.

Comparing the two options it is evident that you are slightly better off if the cylinder is spun.

Probability Roulette Wheel Math

But is this always the case? What if there are two bullets in the gun?

Puzzle 2: Two bullets

In the two bullet version, everything is the same as before except the gun is loaded with one more bullet:

Let’s play a game of Russian roulette. You are tied to your chair and can’t get up. Here’s a gun. Here’s the cylinder of the gun, six chambers, all empty. Now watch me as I put two bullets in the gun. I close the cylinder and spin it. I put a gun to your head and pull the trigger. Click. Lucky you! Now I’m going to pull the trigger one more time. Which would you prefer, that I spin the cylinder first, or that I just pull the trigger?

This problem is a bit trickier because there are different ways the two bullets can be loaded-either in adjacent or not adjacent chambers.

Suppose you were lucky and caught a glimpse of how the bullets were loaded. What should you do?

Suppose the bullets were loaded in adjacent chambers

This problem, similarly, can be solved by considering the odds of survival for the different choices.

First, consider the odds when the cylinder is spun. The cylinder is equally likely to stop at at any of the six chambers. Two of the chambers contain bullets and are unsafe. The other four chambers are empty and you would survive. Consequently, the probability of survival is 4/6, or about 67 percent.

Next, consider the odds if the cylinder is not spun. This situation is a bit trickier so careful accounting is helpful. We know the gun is loaded with two bullets so it has two loaded chambers (let’s label them 5 and 6) and four empty chambers (let’s label these 1, 2, 3, and 4). When the game starts, the trigger is pulled and nothing happens, so we know the cylinder started on an empty chamber. Then, the cylinder advances one chamber forward, meaning the cylinder must now be in one of the positions 2, 3, 4, or 5. If you don’t spin, you will survive in three of these four positions (all but 5). Therefore, not spinning the gun has a probability of survival of 3/4, or 75 percent.

It is now better not to spin, unlike the single bullet case.

Now suppose the bullets are not in adjacent chambers

We proceed as before comparing the two choices.

First, when the cylinder is spun the situation is the same as in the adjacent case. The cylinder is equally likely to stop in any of the six chambers, four of which are empty. Consequently, the probability of survival is 4/6, or about 67 percent.

Next, consider the odds if the cylinder is not spun. This situation again requires careful accounting. We know the gun is loaded with two bullets so it has two loaded chambers (let’s label them 4 and 6) and four empty chambers (let’s label these 1, 2, 3, and 5). When the game starts, the trigger is pulled and nothing happens, so we know the cylinder started on an empty chamber. Then, the cylinder advances one chamber forward, meaning the cylinder must now be in one of the positions 2, 3, 4, or 6. If you don’t spin, you will survive in two of these four cases (4 and 6 are loaded). Therefore, not spinning the gun has a probability of survival of 2/4, or 50 percent. Amazingly this is quite a bit lower than the odds if the bullets were adjacent!

In conclusion, the best choice in the non-adjacent case is to spin.

Possible extensions:

Roulette Wheel Probability Calculator

After going through these puzzles, I was thinking about ways this game could be generalized.

What happens in the case of n bullets? It is easy to compute the probability of survival for spinning (=number of empty chambers / number of total chambers) but what about the probability for not spinning? If you don’t know exactly how the bullets are loaded, is it better to spin or not?

Also, these puzzles have been one-stage analyses. What happens if the game continues with each player alternating the shots, like normal Russian roulette? Does a one-stage advantage allow you to survive longer, or can your opponent use a counter strategy to even the odds?

I have a few ideas and I hope to post my thoughts in the comments later. What are your thoughts?